Проективная плоскость, «с полным её разоблачением»

Гладкая модель проективной плоскости в 5-мерном пространстве (без изломов и самопересечений)
Проективная плоскость в обычной интерпретации — это объект, элементами которого являются обычные прямые, проходящие через какую-либо одну фиксированную точку M в обычном трехмерном пространстве. Если назвать такие прямые p-точками, а плоскости, проходящие через точку M – p-прямыми, тогда через любые две p-точки проходит ровно одна p-прямая, а любые две p-прямые пересекаются в одной p-точке.

Возьмём какую-нибудь сферу с центром в этой точке M. Тогда проективную плоскость можно попробовать представить себе как объект, который получится, если все диаметрально противоположные точки на сфере слепить попарно.

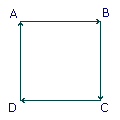По-другому, модель проективной плоскости можно попытаться построить, если склеить попарно стороны квадрата ABCD так, чтобы направленный отрезок AB наложился на CD, а BC — на DA.

В отличие от, например, сферы, это односторонняя поверхность, у неё нет «внутренней» и «наружной» стороны.

В обычном 3-мерном пространстве невозможно построить такую поверхность без самопересечений. В 4-мерном пространстве можно построить модель с особой точкой (остриём).

А в 5-мерном пространстве легко строится гладкая поверхность, реализующая все свойства проективной плоскости.

Пусть x₁² + x₂² + x₃² = 1 –
обычная 2-мерная сфера S в 3-мерном пространстве R³ с координатами (x₁, x₂, x₃).

Рассмотрим такое отображение этой сферы в R⁶:

y₁ = x₁², y₂= x₂², y₃= x₃², y₄= x₁x₂, y₅ = x₂x₃, y₆= x₁x₃

Пусть P – образ сферы S при этом отображении. Ясно, что каждой паре противоположных точек сферы соответствует ровно одна точка в множестве P. Но так как P лежит в 5-мерной гиперплоскости y₁ + y₂ + y₃ = 1, то получаем модель проективной плоскости в 5-мерном пространстве (эта или похожая реализация предлагается в учебнике по дифференциальной геометрии Мищенко и Фоменко).

Чтобы представить, как такая штука может выглядеть, я сделал несколько проекций этого объекта на случайным образом выбранные плоскости. В одном файле – последовательность из 20 таких случайных проекций (скачать GIF-анимацию, около 1 мегабайт). Во втором – большом файле — 450 кадров, при этом плоскости проекции соседних кадров близки (скачать файл – 21 МБ).

Если честно, ясности мне это так не прибавило. Но, возможно, это более наглядное представление, чем на рисунках А.Т. Фоменко.

Обн.: теперь есть ещё и модель проективной плоскости на видео!